社員の売上だったり、学生のテストの点数だったり、色々なシチュエーションでランキングを作りたい時があると思います。
Excelにはもちろんそのような機能が備わっていますので、解説していきたいと思います。

名前のとおりRANK関数でしょ。知ってるよ。

RANK関数にも3種類あるし、RANK関数では対応できない場合もあるのよ。
RANK関数を使って順位を確認する
ExcelにはRANK関数という関数があり、それを使うことで順位を算出、ランキングを作成することが可能です。
3種類のRANK関数
一言でRANK関数と言いましたが、実際は・・・
- RANK関数
- RANK.EQ関数
- RANK.AVG関数
上記の3つの関数があります。まずは下の画像を確認してみてください。
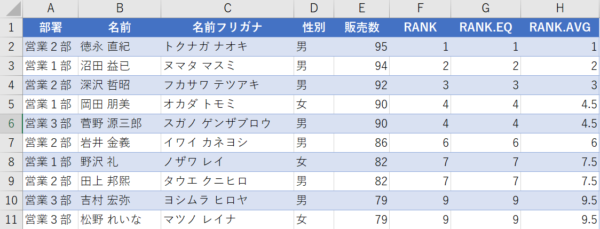
RANK関数(F列)とRANK.EQ関数(G列)は全く同じですね。実は、この2つの関数に違いはありません。(昔はRANK関数しかなかったが、RANK.AVG関数が作られた時に、RANK.EQという新しい名前を付けた ということらしい)
一方、RANK.AVG関数(H列)は結果が違いますね。
例えば、3位の次に同じ点数の人が2人いた場合、RANK(とRANK.EQ)は、4位が2人として扱います。一方、RANK.AVGは4.5位が2人として扱います。つまり、上位の順位に寄せるのか、平均に寄せるのか、という違いですね。一般的には、上位に寄せる方が多いかと思います。
RANK関数の構文
RANK関数およびRANK.EQ関数、RANK.AVG関数の構文は以下のとおりです。
=RANK(数値, 参照, [ 順序 ])
*RANK.EQ、RANK.AVGも同じ構文
引数を今回の例にあてはめて説明すると、こんな感じです。
| 数値 | その社員の販売数 |
| 参照 | 全社員の販売数 |
| 順序 | [0]数値が高い順 [1]数値が低い順 |
順位を求めよう
具体例を示します。
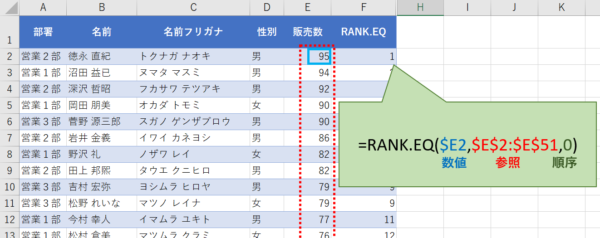
この例では F2 セルに =RANK.EQ($E2,$E$2:$E$51,0) を入力しています。
谷本さんの販売数($E2)は、全50人の販売数($E$2:$E$51)のうち、何番目に大きいか という意味になります。
これで、順位が算出できたので、並べ替えしちゃえば無事ランキングが作れますね。

先輩~!販売数ランキングが作成できました!

う~ん・・・たしかにランキングが出来ているけど、部署内での順位も知りたいわね・・・。
COUNTIFS関数を使って、グループ(部署)内の順位を算出する

ん~・・・じゃあまたRANK関数でどうにかするか~。
・・・・・・・できない。
RANK関数は、簡単で便利ではあるのですが、こういった応用には使えません。
今回は COUNTIFS関数を使って、部署ごとの順位を算出したいと思います。
COUNTIFS関数について
COUNTIFS関数は、指定した条件に合致するデータがいくつあるのかを求める関数です。なお、「条件」は複数個指定することが可能です。
COUNTIFS関数の構文は以下のとおりです。
=COUNTIFS( 検索条件範囲1, 検索条件1, [ 検索条件範囲2, 検索条件2,・・・] )
部署が自分と同じで、なおかつ、販売数が自分より多い社員の人数に1を足せば、自分の順位がわかりますよね。それをCOUNTIFSで求めればよいのです。
順位を求めよう
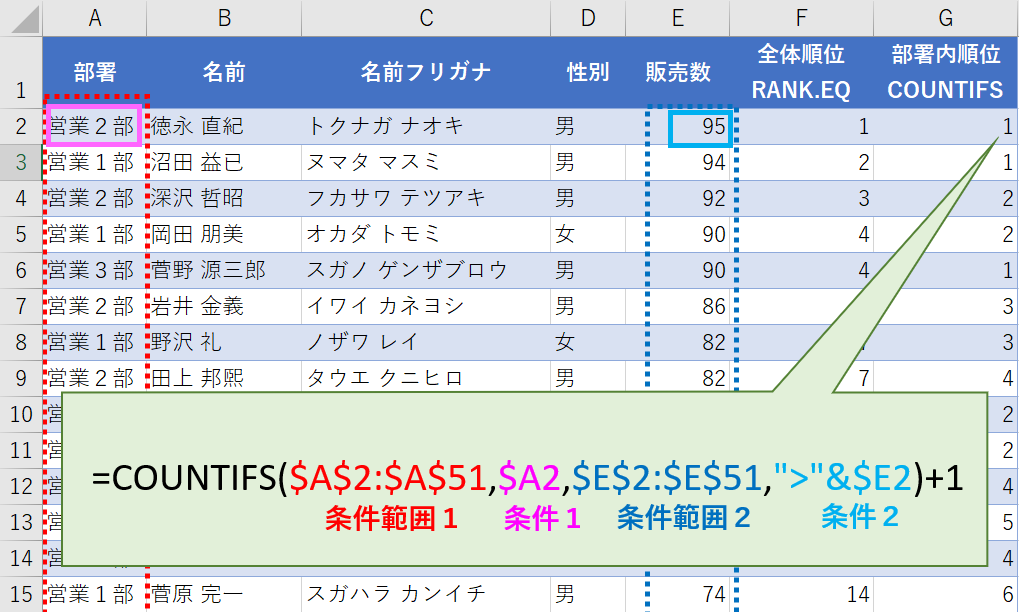
実際の式は =COUNTIFS($A$2:$A$51,$A2,$E$2:$E$51,“>”&$E2)+1 となりました。
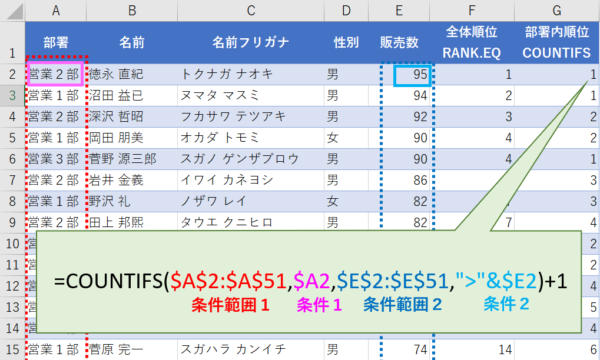
1行目の徳永さんの例では、部署が”営業2部”で、販売数が95より多い人数(+1)という意味になります。

条件2の「 “>”&$E2 」が意味がわからないのですが・・・
COUNTIFS関数では、大なり(>)、大なりイコール(>=)、小なり(<)、小なりイコール(<=)、ノットイコール(<>)などの比較演算子を使うことができます。
この例だと、「$E2の値より大きい」としたいので、“>” と $E2 をアンドでつないで、「 >$E2 」を実現しているのです。

ふ~ん。じゃあ、最後に+1するのはなぜ?
具体例で考えましょう。例えば販売数3位の人は・・・
自分より販売数が多い人は2名。つまりCOUNTIFSの結果が2となる。でも順位は3位だから、+1をする必要があるのです。
おわりに
”ランキング” や ”順位” を算出する仕事だ、と思ってしまうと、RANK関数を使うことだけに目が行ってしまいがちです。
今回の例だけでなく、色々な関数が色々な場面で役に立ちますので、考えを固定せずに柔軟に捉えることと、引き出しを増やしておくことが大事だな、と思いました。

コメント